CPA FRM - Module 4: Derivatives | KnowledgEquity
- Angela

- Nov 8, 2020
- 6 min read
By the end of this module you should be able to:
explain what is meant by ‘derivatives’ and the role of derivatives in financial risk management
describe the four main classes of derivatives
explain the basis on which derivatives are priced and valued, and calculate the relevant values
describe exotic derivatives and hybrids.
three most common ways of using the derivatives for hedging include: foreign exchange risk, interest rate risk, and commodity or product input
Which of the following best describes our financial derivative?
a financial instrument used to control financial risk
a financial instrument whose value changes based on the value of an underlying asset
a financial instrument involving a buyer and a seller obligating the buyer to buy at a predetermined price
Derivative - IFRS 9
A derivative is a financial instrument... with all three of the following characteristics:
its value changes in response to the change in a specified... variable... {the 'underlying']
it requires no initial net investment or... [relatively small] initial net investment [given the exposure it provides]
it is settled at a future date
Type of contract > Underlying variable
Interest rate swap > Interest rates
Commodity option > Commodity prices
Currency option > Foreign exchange rates
Forward exchange contract > Foreign exchange rates
Sales contract with inflation adjustment > Consumer price index (CPI)
Purchase contract with repricing clause > e.g Interest rates or foreign exchange rates
Types of derivatives
1. Real derivatives
"real options"
relates to business initiatives and activities
e.g. deferring, abandoning, or expanding a capital investment project
choices or opportunities are based on changing economic, technological or market conditions
e.g. opportunity to build a new manufacturing plant, which also provides real options for developing new projects and distribution channels
timing options (when)
exit options (opt out)
operating options (adjust)
2. Commercial options
"synthetic derivatives"
relates to commercial contracts
rights to adjust terms and conditions
repricing closest
inflation adjustments
on costing
3. Financial derivatives
financial contract
value derived from another financial instrument or a market index
Financial derivatives - 4 main classes
forwards: buyer and seller enter into a contract which places an obligation to buy and sell an asset at an agreed price at an agreed future date (a private transaction)
futures: standardised forward contract that is traded on an exchange - not a private transaction
swaps: two parties exchange cash flows from one asset for the cash flows from another asset
(swap arrangement example: floating interest rate - fixed interest rate)
options: buyer has the right to buy or sell an asset at an agreed price on or before a future date, the seller has an obligation to sell or buy the asset
4.1 Forwards
forward exchange contract
very flexible, able to be tailored
no upfront costs, but real, immediate exposure
credit, market liquidity and settlement risk
cash on physical delivery
E.g.
foreign exchange forward
interest forward
commodity price forward
The current AUD/USD spot rate is 0.8500 and the forecast rate for six months' time is AUD/USD 0.8000. if you enter into a foreign exchange forward today with settlement in six months, what will the forward rate be?
The current AUD/USD spot rate is 0.8500
the forecast rate of AUD/USD 0.8000
Neither of these options
the forward rate is not a forecast rate. It is calculated using a formula based on the current spot rates, interest rates and days to maturity
Spot rate ("on the spot"):
the current price or bond yield
In commodities futures markets - the price for a commodity being traded immediately
Forward rate ("forward-looking"):
In commodities futures markets - settlement price of a transaction that will not take place until a predetermined date
In bond markets - the effective yield on a bond, commonly U.S. Treasury bills, and is calculated based on the relationship between interest rates and maturities.
4.1.1 foreign exchange forwards
buy or sell a specified amount of foreign currency at an agreed rate at a specified future date

forward rate is not a spot rate forecast
Quiz 2. Company A enters into a 2 x 8 forward rate agreement (FRA) with its bank, for a six-month borrowing, starting in two months' time.
The FRA rate is set at 5%. In two months' time, the sixth-month reference rate is 5.50%. What will occur at maturity of the FRA?
Company A will pay the bank the difference between the notional interest amounts
The bank will pay Company A the difference between the notional interest amounts
Company A will pay the fixed rate to the bank and receive the floating rate from the bank
The FRA locks in a borrowing rate of 5% for a Company A for the future 6-month period, starting in 2 months' time.
If the reference rate is higher (i.e. 5.5%) then the bank pays Company A the difference in notional interest amount (i.e. 0.5% for the 6 month period).
Company A would then enter into the borrowing at the higher interest rate of 5.5% but the effective or net rate is the locked-in 5%.
If the reference rate was lower (4.5%), then Company A would pay the bank the difference in notional interest amount (i.e. 0.5% fo the 6 month period).
Company A would then enter into the borrowing at the lower interest rate of 4.5% but the effective or net rate is the locked-in 5%.
4.1.2 interest rate forward
borrow or lend at an agreed rate beginning on a future date for an agreed term - "cash settled'
4.1.3 commodity price forward
underlying asset is a commodity - metals, soft, energy, etc
Quiz 3. You enter into a commodity price forward agreement to buy wheat at USD 100 per tonne. The current spot price is USD 95 per ton. What is this an example of?
Contango*
Backwardation**
Commodity speculation
*Contango: forward price is greater than current spot price (typically non-perishable, e.g. metals, that have a carry cost)
**Backwardation: forward price is lower than current spot price (temporary supply disruptions or demand increases, fear of falls)
4.2 Futures
Uses
Hedging
Speculation
Arbitrage
Standardised contracts (hedging inefficiency)
initial deposits and ongoing margins
Clearing house is the counterparty (lower risk)
Cash or physical delivery, but usually 'close out'
4.3 Swaps
swap one obligation for another
e.g. fixed interest for floating interest
most common derivative in use
time value of money
Quiz 4. Company A has a $100,000 floating rate (BBSW) loan. It wants to protect against the interest rates rising and decides to fix the rate at 5.5% by entering into a fixed-for-floating interest rate swap with TYM Bank, with annual swap periods.
If the BBSW is 5.75% at the next swap date, what will Company A's effective borrowing rate be?
5.50%
5.75%
borrower:
protect against rising interest rates (pay fixed)
participate in falling rates (paying floating)
lender:
protect against falling rates (receive fixed)
participate in rising rates (receive floating)
Quiz 4. Company A has a $100,000 floating rate (BBSW) loan. It wants to protect against interest rates rising and decides to fix the rate at 5.5% by entering into a fixed-for-floating interest rate swap with TYM Bank, with annual swap periods.
If the BBSW is 5.75% at the next swap date, what will Company A pay to TYM Bank and/or receive from TYM Bank under the swap?
Pay $250 to TYM Bank only
Receive $250 from TYM Bank only
Pay $5,550 to TYM Bank and Receives $5,750 from TYM Bank
Pay $5,750 to TYM Bank and Receives $5,550 from TYM Bank
In an interest rate swap, the principal amount of $100,000 is a 'notional amount' (it is not swapped). Further, only the net interest differential is transferred between the swap parties.
Company A is paying fixed @5.5% = $5,500
TYM Bank is paying floating @ 5.75% = $5,700
TYM Bank is therefore required to pay $250 to Company A.
Interest rate swaps
exchange interest on a principal sum that is not exchanged
simple interest calculation
net interest differential paid
zero coupon rate used for pricing
4.4 Options
seller on the other side has the obligation to sell or buy the asset
buyer pays a premium
could be physical commodities, interest rate, foreign exchange or interest rate swaps
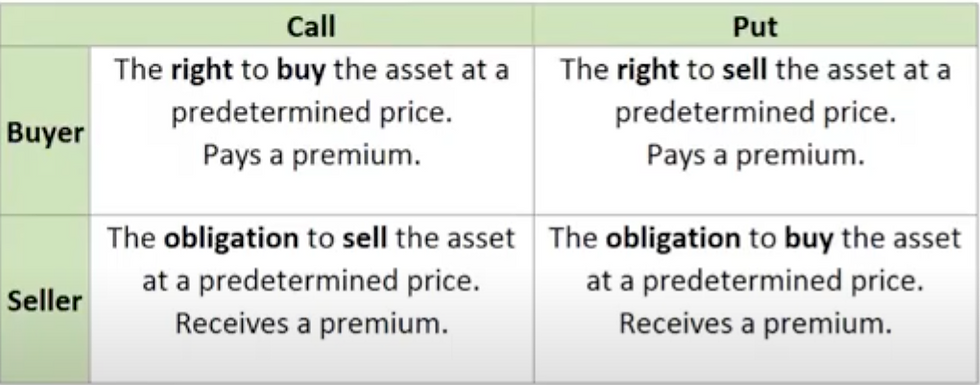
Long call
bought call option (paid premium to seller)
buyer has the right to buy the underlying asset at the strike price
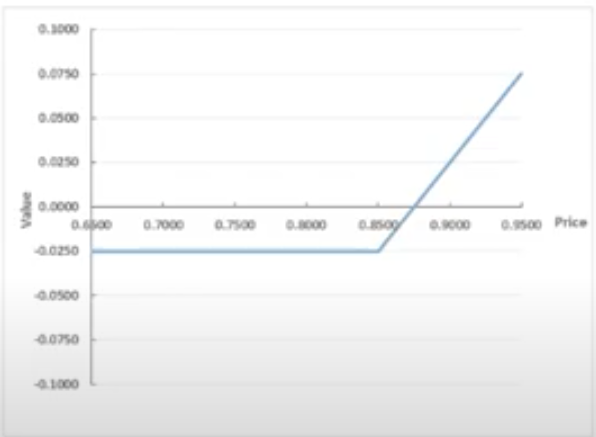
Short call
sold call option (received premium from buyer)
seller must sell the underlying asset at the strike price (if the buyer exercises their right to buy)
Long put

bought put option (paid premium to seller)
buyer has the right to sell the underlying asset at the strike price
Short put
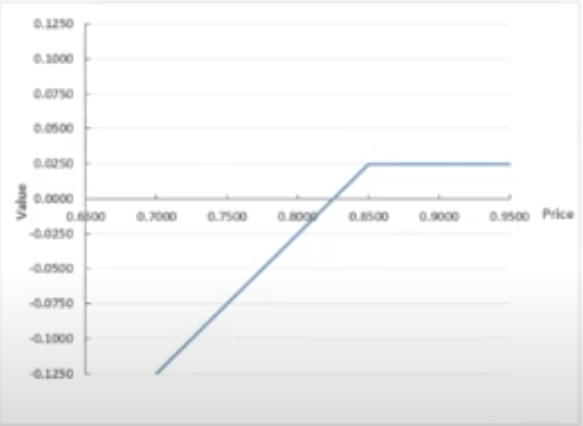
sold put option (received premium from buyer)
seller must buy the underlying asset at the strike price (if the buyer exercises their right to sell)
Activity - pay-off diagrams
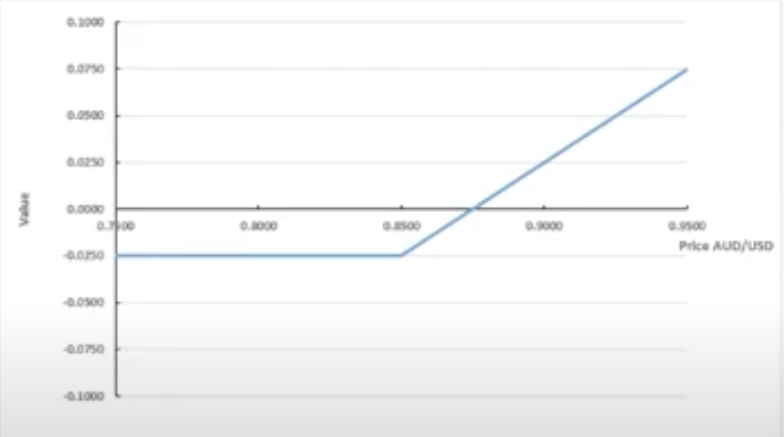
As the assistant treasurer at CBF Limited you have just assisted in the purchase of an AUD call/USD put option.
The pay-off diagram for this option is presented to right.
Based on the pay-off diagram, answer the following questions:
What is the strike price for this option?
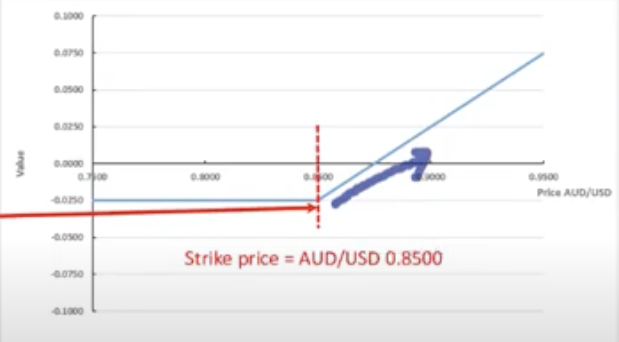
What is the option price, or premium?
$0.0250, the buyer paid to compensate the seller for the risk the seller was taking
What does this option allow CBF Ltd to do, and why would CBF enter into such an option?
CBF wants to protect against rising AUD - maximum AUD/USD 0.8500
exporter - receiving USD and converting to AUD
as the AUD/USD rises, the exporter receives less AUD
but this is offset by the increasing value of the AUD/USD call option
If at the maturity date the spot price is AUD/USD 0.8900, should CBF Limited exercise the option? If so what would be the effective rate for CBF limited?
Exercise at strike price (0.8500) BUT
Effective rate = strike price + premium
= 0.8500 + 0.0250 = 0.8750
Option pricing
Intrinsic value: generally where forward price is higher than strike price
Time value
Option pricing - call option example
Days remaining 90 60 0
Forward price $80 $80 $80
Strike price $75 $75 $75
Option price $ 8 $ 7 $ 5
Intrinsic value* $ 5 $ 5 $ 5
Time value** $ 3 $ 2 $ 0
*intrinsic value
"in-the-money" options
= forward price - strike price
**time value
remaining premium in excess of intrinsic value before the option expires
probability that the option's value will increase before expiry
time value is zero at expiry
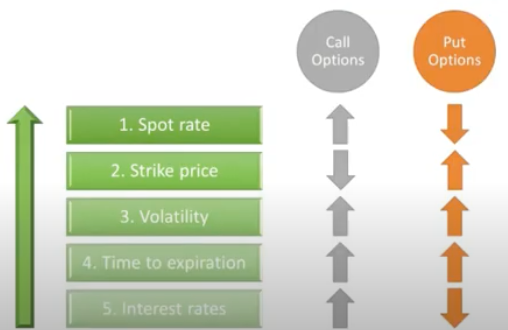
Price determinants
exotic derivatives
081120




Comments